Organic Ribbon Geometry

Geometry
,
1

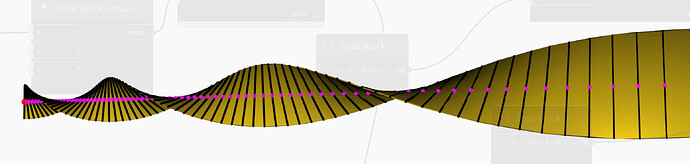
image
image711×556 65.9 KB

Can anybody help me model something like this in dynamo?

1 Like
2
  1. Draw the line showing the path of the ribbon.
  2. Curve.CoordinateSystemAtParameter from 0 to 1, with the desired number of steps.
  3. CoordinateSystem.XYPlane to get the rotation plane.
  4. CoordinateSystem.Rotate to rotate each coordinate system about their XY plane by a range of degrees from 0 to 720, with the desired number of steps.
  5. Draw a rectangle with the desired disjoins on the XY plane with a Rectangle.ByLengthWidth node.
  6. Geometry.Transform to put the rectangle into the position defined by each coordinate system.
  7. Solid.ByLoft to define the ribbon geometry.
7 Likes
3

@jacob.small @gvero774 ,

i did it slidly diverent…

image
image2409×573 174 KB

LoftBone.dyn (36.5 KB)
LoftBone
LoftBone4652×1190 317 KB

KR
Andreas

8 Likes
4

Second topic along these lines. Do try to submit a work in progress attempt for future ones if you can - it goes a long way in making people more inclined to assist (+ nice work Andreas!).

2 Likes
5

Rather than intimidate beginners, I hope this serves a motivation to explore Design Script :slight_smile:

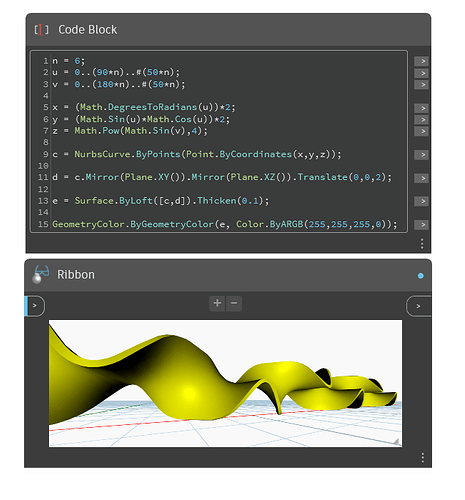
ribbon_2023-08-25_06-24-25
ribbon_2023-08-25_06-24-25652×700 63.9 KB

n = 6;
u = 0..(90*n)..#(50*n);
v = 0..(180*n)..#(50*n);

x = (Math.DegreesToRadians(u))*2;
y = (Math.Sin(u)*Math.Cos(u))*2;
z = Math.Pow(Math.Sin(v),4);

c = NurbsCurve.ByPoints(Point.ByCoordinates(x,y,z));

d = c.Mirror(Plane.XY()).Mirror(Plane.XZ()).Translate(0,0,2);

e = Surface.ByLoft([c,d]).Thicken(0.1);
7 Likes
6

avesome :wink:

1 Like
7

@Vikram_Subbaiah ,

how the hell you come to this poem ? of design script ? do you even think ? or it comes directly from the universe :slight_smile:
KR
Andreas

2 Likes
8

@Draxl_Andreas
Its mostly manipulation of the Sine Curve :slight_smile:
Note the multiplication and exponentiation of the x, y and z values in the second block of code that manipulates the profile of the points/curve

2 Likes