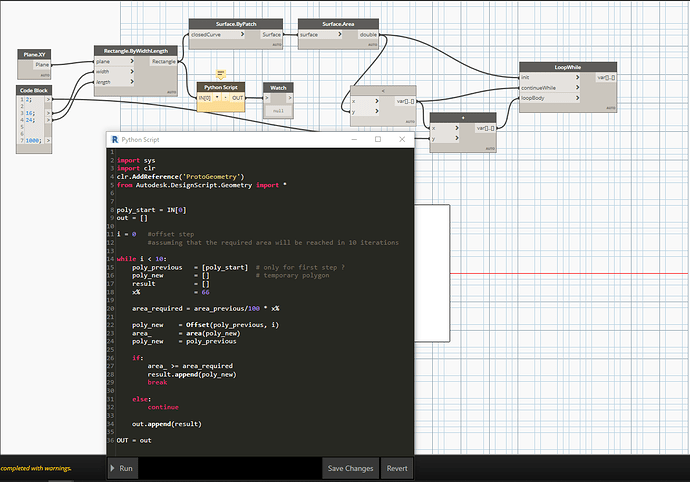
Hi,
I think this problem could be solved with ‘while loop’. I am new to python so I wrote the problem in english / gibbresh 
I have a polygon and I want it to keep offsetting inside till the area becomes the x% of the initial polygon area ( lets say 66% ) of initial area.
Logically it sounds easier. But I could not trace it. I tried nodes as well, no luck so far. Any help would be appreciated.
Thanks in advance to any hero
I’d get my original input polygon and calculate it’s area.
Inside the loop I’d:
Offset my polygon and recalculate area
if the area was what I wanted this would be my out
if the area was not what I wanted I’d loop again
Remember as you try to tackle this offset that it’s pretty much a certainty that you won’t hit that 66% of the original area by repetitive offset. Ideally you’d utilize an alternative solution (ie: scale the original shape), or set a range of allowable between say 65% and 67%.
2 Likes
@ Alein, thanks for looking into it. Your solution prompted me to go through ’ Shoelace algorithm for area’, I never really looked into how area of polygons is calcualted by Cartesian coordinates.
its embarrassing for me that I couldn’t get the results even after reproducing your solution . Could you please have a look in where am I making a mistake. I am getting 0 all areas if i use you method. And I get values in -ve when I remove round(). I am sure I am overlooking something.
My Revit model is in mm.
@ Alien, it worked on model set to mm.Thanks
I tried playing around with 100 00 00 value with model unit set to meters but didnt got any offset. I am just curious what is actually happening. As i understand, the offsetted line stays where it was.
The 1000000 value is 1000mm squared; change it to 1 and see if that works.
Thanks, it worked. I have to turn the accuracy to 1 as well.
@Alien - Very cool solution! I wrote a similar python node that for another post that uses offset to get to a target surface area (which you get using the percentage calculation in this case). The main difference between the solutions, is that you are using a linear step for the resolution, and I used half steps which makes the curve more logarithmic.
I’m inspired to see how you made your own surface area calc! I would suspect it’s more performant than the alternate surface by patch, then get area.
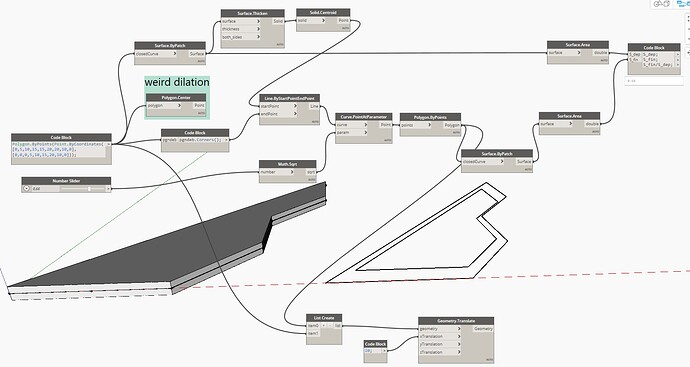
Hello,
here is a dilation approach
11 juillet forum anglais.dyn (31.2 KB)
But the offset is not regular
cordially
christian.stan
1 Like
Very cool!
I think this is similar to what @jacob.small was recommending, where you would effectively scale the shape for the exact calculation.
Seems like the centroid z offset from thickening had insignificant impact on the area calc. If it was pulled to the same z, i would suspect that it still works.
It’s elegant how it’s executed with just a few nodes!
1 Like