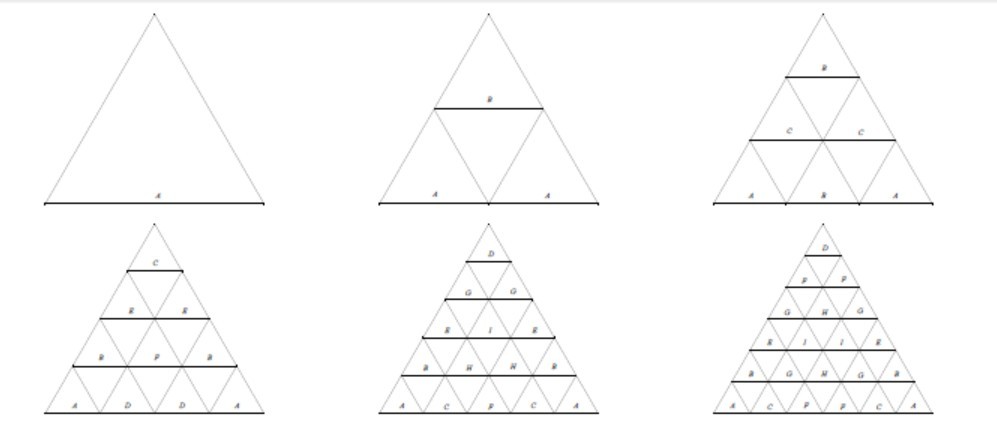
The math to understand the uniform subdivision of a triangle which results in its square is well-known and is easy to produce geometrically with pen and paper (see above). I’m running into obstacles when trying to code such funcationally in Dynamo/Designscript. Searching the forums for help it doesn’t appear this question has been addressed before and I could really use the help. I’m not above using previously published packages but even when I try to study and understand them I’m having trouble getting them to work.
I’m hoping to get a node working that takes surfaces, divides them, and then outputs them as surfaces again. Thanks.
2 Likes
Hi @PerfectArchCo ,
How about this :
The first function performs a subdivition of one triangle, the second fonction iterates the first one as many times as you want to .
2 Likes
Thank you so much for your effort but unforuately - though it might be a very salient point - it’s not quite mathmatically what I’m looking for. I already wrote code - though not as elegant as yours - which iterates triangles upon themselves. However, that subdivision method will only ever produce subdivisons based on the powers of 2 - 2,4,8,16 etc - and not the full list of intergers as per the image - 2,3,4,5 etc.
It’s striking that this is rather trival to do with pen and paper but turns out to be quite difficult computationally - at least for me - but I love math and this is a great challenge.
This topic might give you some ideas:
Here is a start (half the number of sub triangles created) …
equilateralSubDivision.dyn (4.2 KB)
Complete definition …
equilateralSubDivision.dyn (4.9 KB)
3 Likes
Just for the sake of having a little fun 
here’s a less geometric / more arithmetic way to see it:
if you look at a 2n+1 dimension matrix :
XOXOXOX
OXOXOXO
OOXOXOO
OOOXOOO
the pattern of the regular subdivision of an equilateral triangle goes :
0 2 4 … 2n+1
1 3 5 … 2n
2 4 6 … 2n-1
.
.
.
n+1
here’s a way to describe it in design script:
subdiv matrix.dyn (4.5 KB)
4 Likes
Thank you so much for taking the time to offer your ideas. I wish I could grant more than one solution. Hopefully others in the future facing this same question can find this threat. I think it will help a lot of people build. 

I’m excited to try and run this code into my script this week. I’m concerned about transplanting it into my larger script. I’ll report back if I have any problems.
1 Like
The matrix method unfortunately doesn’t appear to orient to the surface I’m hoping to divide however when testing the other code before passing through my 20 surfaces I’m getting a strange offset on each subdivided triangle which is not in the example. I assume it has something to do with either Translate and “dirX” functions or the n2/n3/n4/n5 steps but when investigating against the original couldn’t see anything amiss. (Running the original dyn file on my system works as expected.)
Hi @PerfectArchCo
In order to get the matrix to adapt to the orientation of your surfaces, you can use coordinate systems. Here’s a code that will work wathever the orientation of your tirangle is  :
:
//setting the coordinate system
p = s.PerimeterCurves();
l = p[0].Length;
h = l*Math.Sin(60);
pts = p.StartPoint;
csx = Vector.ByTwoPoints(pts[0],pts[1]);
csy = Vector.ByTwoPoints(pts[0],pts[2]);
cs = CoordinateSystem.ByOriginVectors(pts[0],csx,csy);
//creating matrix
n = subdivn*2+1;
rangex = 0..l..#n;
rangey = 0..h..#n;
matrix = Point.ByCartesianCoordinates(cs,rangex<2>,rangey<1>,0);
tripoints = List.TakeEveryNthItem(matrix,2,1);
//generating arithmetic suites
indx = 0..subdivn+1;
indy = n..subdivn+1;
suites = indx..indy..2;
//building triangles
pts2 = List.GetItemAtIndex(tripoints<1>,suites<1>);
c = List.Count(pts2<1>);
pts3 = List.Clean(List.GetItemAtIndex(pts2<1>,((0..c-1)..(1..c-1))<1>));
pts4 = List.DropItems(pts2,1);
corners = List.AddItemToFront(pts4<1><2>,pts3<1><2>);
Triangles = PolyCurve.ByPoints(corners,1);
//Using polysurface to split initial triangle
polysurf = PolySurface.ByJoinedSurfaces(Flatten(Triangles.Extrude(1)));
s.Split(polysurf);
You just neet to feed it your initial surface and the number of subdivisions. Hope this gets you where you want
subdiv matrix coordinate system.dyn (6.0 KB)
3 Likes
Check if the surface you are feeding in is equilateral.
Altered the file I’d provided above to accept an equilateral surface.
equilateralSubDivision.dyn (4.9 KB)
2 Likes
This is a very interesting problem. And I’ve seen that has very good solutions here.
I would also like to present another approach in order to be discussed.
I did this using another way taking the coordinates of the vertices of the main equilateral triangle, so that no matter their position in space.
It also returns the (x,y,z) of the vertex of each sub-triangle that can be used for panelling.
My ultimate goal was to build a parameterized geodesic dome. And I got. I used this Tom Davis
paper as a reference. geodesic dome.pdf (564.8 KB)
This triangulation was part of the process.
triangulacao-v07.dyn (30.9 KB)

1 Like
Looking sharp @Vikram_Subbaiah.
Interestingly @Ricardo_Freitas I have that paper printed off and sitting within arms reach already. Unforuately that paper doesn’t cover how he subdivided the surface but then again, Dynamo is just so cool, who wouldn’t want to try it? I agree there’s lots of good approaches here and hopefully it will become a good resource for the forums.
1 Like
Obtaining the points of the sub triangles is quite easily done by getting the vertices of the polygons/surfaces
1 Like
Just adding to the resource 
Modified the definition to process a list of equilateral triangle surfaces of different sizes
equilateralSubDivision1.dyn (5.3 KB)
The above code fails when the number of sub divisions is less than 2.
Here is a rectified version that addresses the issue …
//Edges of equilateral surface
crv1=tri.PerimeterCurves();
len1=List.GetItemAtIndex(crv1<1>,0).Length;
n=d<1?1:d;
len2=len1/n;
//Vertices of equilateral surface
pnt1=List.GetItemAtIndex(crv1<1>,0).StartPoint;
pnt2=List.GetItemAtIndex(crv1<1>,1).StartPoint;
pnt3=List.GetItemAtIndex(crv1<1>,2).StartPoint;
dir1=Vector.ByTwoPoints(pnt1,pnt2);
dir2=Vector.ByTwoPoints(pnt1,pnt3);
dir3=Vector.ByTwoPoints(pnt2,pnt3);
//Sub triangle 1
pnt4=pnt1.Translate(dir1,len2);
pnt5=pnt1.Translate(dir2,len2);
sub1=Polygon.ByPoints(Transpose({pnt1,pnt4,pnt5}));
//Repeating sub triangle
n2=(0..(n-1))*len2<1>;
sub2=sub1.Translate(dir1,n2);
n3=List.TakeItems(n2<1>,1..n);
sub3=sub2.Translate(dir3,n3);
//Sub triangle 2
pnt6=n<2?pnt1:pnt4.Translate(dir2,len2);
sub4=Polygon.ByPoints(Transpose({pnt4,pnt5,pnt6}));
n4=(0..(n-2))*len2<1>;
sub5=sub4.Translate(dir1,n4);
n5=List.TakeItems(n4<1>,1..n);
sub6=sub5.Translate(dir3,n5);
srf1=Display.ByGeometryColor(sub3.Patch(),Color.ByARGB(255,115,200,26));
srf2=Display.ByGeometryColor(sub6.Patch(),Color.ByARGB(255,105,100,26));
srf11=Flatten(List.TakeItems({srf1,srf2},n));
sub21=Flatten(List.TakeItems({sub3,sub6},n));
Shows yes, read more carefully.
First you need an icosahedron and a co-centric sphere to him.
Then subdivided each face of the icosahedron with one of the methods shown here in order to obtain the vertices of each sub-triangle.
Then make the projection of each point on the surface of the sphere.
Now redo each sub-triangle with the projected points.
This is the procedure that Tom says in his paper.
It’s a brilliant idea right? I was very happy when I could do it.
The hardest part is actually making the sub-divisions.
1 Like
This earlier geodesic post might interest you - The icosahedron method
1 Like
Returning to your question about the surface being equilateral, it appears my surface is not equilateral. The watch node is displaying the magenta curve lengths. It appears only the top ones are offset and unequal as the lower ones are equal and tight to each other.
Would you suggest I go back and tweak the code which genorates the icosahedron? I don’t mind doing it. This stuff is just too much fun. I’m also going to experiment with some of the other impliminations to see what else I can learn.
Edit: it appears the maxtix approach fails for the same unequal triangle condition. Fascinating…
Does seem like the icosahedron code requires rectification