Actually the question in the subject. Thanks in advance.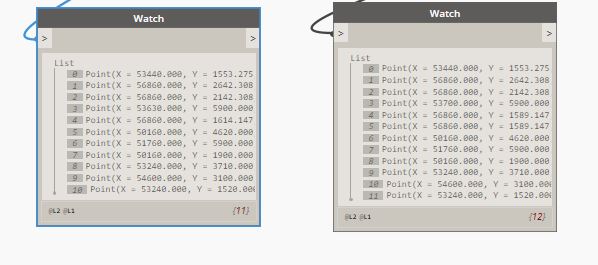 
I need to build lines between points in the same plane and do it in the Python script.
Something like this:
same plane means that either they will have the same X,Y, or Z. so you can group them by it. Then sort the point by magnitude in ascending/descending order and just draw lines by points.
For example, you grouped them by X plane. means you will need to find the magnitude of Y and Z axis and hence sort them accordingly and vola, you can plot a lines by points
Thank you, but this implementation does not suit me.
A similar thought occurred to me, but it seems to me that the idea itself is not perfect.
I wanted to build lines between two lists and find lines with a minimum length, provided that the end point is unique.
may i know what is your application? by two list you mean you will need to have cross multiplication of lines??
There are two lists in the picture. The starting points are 1, the end points are the second. Total 11 * 12 = 132 lines. After the selection there will be 12 lines I need. But, although this solves the problem, it seems to me not an ideal solution.
Note: Although the lists contain matching values for X Y, the values may differ in reality.
Lines before sorting
so you just wanna get the shortest distance between point1 to point2, point2 to point3, point3 to point4??
Can you post your dyn so we can build from a common start point? Its hard to understand exactly what the problem is, and and even harder to understand what the starting point for your data is. Providing the later might remove the need for the former.
I’ll post a python script solving problem. Input parameters are two sets of points in the apartment. Socket box and the sockets themselves.
The problem is that the solution seems too unreasonable to me.
#
import clr
clr.AddReference("ProtoGeometry")
from Autodesk.DesignScript.Geometry import *
clr.AddReference("RevitNodes")
import Revit
clr.ImportExtensions(Revit.Elements)
clr.ImportExtensions(Revit.GeometryConversion)
clr.AddReference("DSCoreNodes")
from DSCore import *
ps1 = IN[0]
ps2 = IN[1]
lak1=[]
pak1=[]
pak2=[]
for f in range(len(ps2)):
for ff in range(len(ps1)):
lak2=[]
lak2.append(ps1[ff])
lak2.append(ps2[f])
lak1.append(lak2)
for ff in range(len(lak1)):
pak1.append( PolyCurve.ByPoints(lak1[ff]))
######
for fff in range(len(pak1)):
f1=pak1[fff].PointAtParameter(0)
f2=pak1[fff].PointAtParameter(1)
lll=Line.ByStartPointEndPoint(f1,f2)#.ToRevitType ()
pak2.append(lll)
s1=[]
for b in range(len(pak2)):
s2=[]
s22=[]
s23=[]
for bb in range(len(pak2)):
s3=[]
if Circle.ByCenterPointRadius(pak2[b].PointAtParameter(1),10).DoesIntersect(Circle.ByCenterPointRadius(pak2[bb].PointAtParameter(1),10)):
s4=[]
s22.append(pak2[bb])
s23.append(pak2[bb].Length)
h7=min(s23)
h8 = s23.index(h7)
s4.append(s22[h8])
s3.append(s4)
s1.append(s3)
sss=List.Flatten(s1,1)
sss1=List.Flatten(sss,1)
sss2=set(sss1)
OUT =sss2
So you’re trying to get the sockets that are co-located on the socket boxes? Would it work if you got the bounding boxes of the socket boxes and then get sockets that intersect those bounding boxes?
- Yes.
- I do not understand the question.
I have a distance from the box to the outlet is always the minimum. Outlets can be several on the box and they can be located in different coordinates along the axes.
In figure PAK1, lines connecting the box with all the sockets are constructed. On sss2, the filter is the minimum distance and this is the correct solution to the problem (the presented script is my solution). But…
2.1. I think this solution is not effective.
2.2. By implementing the solution, you can “throw stones” at me
I will add …
According to the presented logic, I need to first build the connections, then filter, and due to the fact that the points do not coincide due to rounding through “Circle.ByCenterPointRadius”, but my not knowing, also led to the construction of “Line.ByStartPointEndPoint” after "PolyCurve. ByPoints ".