Hi,
I searched on the web for a solution to obtain an optimization of optional points from the starting point to the end point, without exceeding a given distance (500cm).
I saw the agorithm Travel Selman Problem with its Ramer-Douglas-Peucker variants. Maybe a node or code can answer my need.
Without knowledge of Python, and from that I tried with ChatGPT but I reached the limits without having a suitable result.
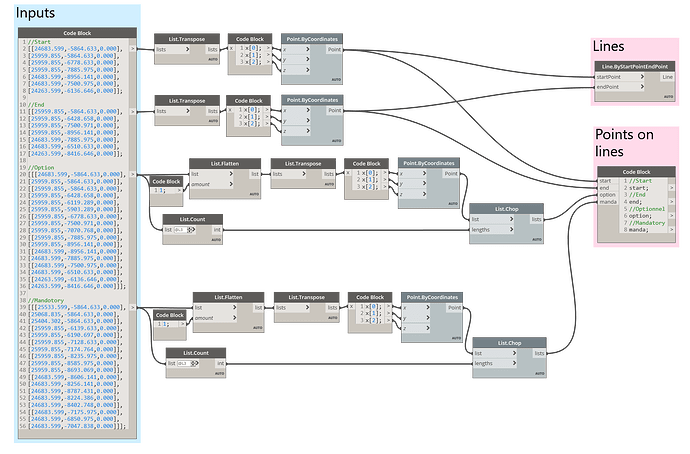
My input lists of the same length, sometimes nested with:
- starting points
- arrival points
- optional crossing points
- obligatory point (mandatory)
I am attaching data for example, have you any idea how I can optimize optional crossing points ?
Connect_dots.dyn (49.4 KB)
Thank you
Look into the minimum spanning tree algorithms in the Topologic package as a starting point. 
I try Topologic package, I don’t see how to use the minimum spanning tree algo in my case, I took a screenshot of expected result.
Yellow points are optionnal crossing points
Red points are mandatory if optionnal points are less 500cm, I delete it.
I looked on Topologic learning page the Minimum Spanning Tree and Shortest Paths By Key graph but I don’t see how can I build a dictionary ?
And does Topologic cumulative sum and/or iterate operations ?
I believe Dictionary.ByKeysValues should do the trick.
I think this depends on the specific minimum spanning tree implementation. What have you used? Best to post a data set, your graph, and a canvas export of the graph after expanding data previews and zooming in on a node. Otherwise we can only talk theory.
I know the node Dictionary.ByKeysValues do a dictionary, I don’t see which values with key I should associate 
I looked up, didn’t use the Minimum Spanning Tree and Shortest Paths By Key graph on Topologic learning page, I can’t get inspired to adapt the graph to my case.
On my 1st post, I upload a graph (see the screenshot), is this OK ?
That upload is fine if you haven’t managed to build a topological implementation yet.
I am away from my PC, but I recall the shortest path requires a topological wire to start with. So the first step is implementing that, and then you can start looking into the subsequent problems.
I will note that it is hard to conceptually link your Revit screenshot with the salesman issue, as you appear to have a linear sequence (meaning each point is connected to the one before it in the line and the one after it, but no others, along a single route) not a true network (meaning point N is connected to M other points). If this is the case you might be looking to build bins of lengths up to a given size.
1 Like