Hi,
I stumbled upon a difference in behaviour between DesignScript and Python while trying to perform simple mathematical operations. Python yields the correct result (checked in a 3rd party software) while DesignScript produces a non-sense result. I suspect that i use Math library in a wrong way. i attach code in both languages below.
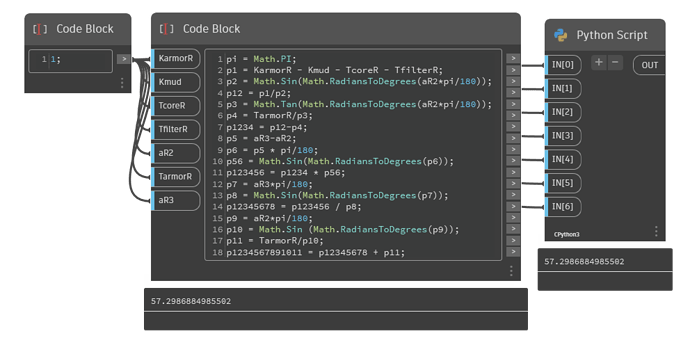
DS:
pi = 3.14;
p1 = KarmorR-Kmud-TcoreR-TfilterR;
p2 = Math.Sin(aR2*pi/180);
p12 = p1/p2;
p3 = Math.Tan(aR2*pi/180);
p4 = TarmorR/p3;
p1234 = p12-p4;
p5 = aR3-aR2;
p6 = p5 * pi/180;
p56 = Math.Sin(p6);
p123456 = p1234 * p56;
p7 = aR3*pi/180;
p8 = Math.Sin(p7);
p12345678 = p123456 / p8;
p9 = aR2*pi/180;
p10 = Math.Sin (p9);
p11 = TarmorR/p10;
p1234567891011 = p12345678 + p11;
Python:
KarmorR = IN[0]
Kmud = IN[1]
TcoreR = IN[2]
TfilterR = IN[3]
aR2 = IN[4]
TarmorR = IN[5]
aR3 = IN[6]
# Place your code below this line
pi = math.pi
p1 = KarmorR - Kmud - TcoreR - TfilterR
p2 = math.sin(aR2*pi/180);
p12 = p1/p2;
p3 = math.tan(aR2*pi/180);
p4 = TarmorR/p3;
p1234 = p12-p4;
p5 = aR3-aR2;
p6 = p5 * pi/180;
p56 = math.sin(p6);
p123456 = p1234 * p56;
p7 = aR3*pi/180;
p8 = math.sin(p7);
p12345678 = p123456 / p8;
p9 = aR2*pi/180;
p10 = math.sin (p9);
p11 = TarmorR/p10;
p1234567891011 = p12345678 + p11;
# Assign your output to the OUT variable.
OUT = p1234567891011
I am pretty sure I might be using syntax of DS in a wrong way, but I am unable to localize the issue myself. Anyone has suggestion where to look for a solution? Also, I couldn’t find any documentation on Math library, anyone knows if it exists in DS?
Thanks!