Splitting a line

Revit
1

Hi everyone,
I need help with splitting a line in Dynamo. Here’s my situation:
What I Need to Do:
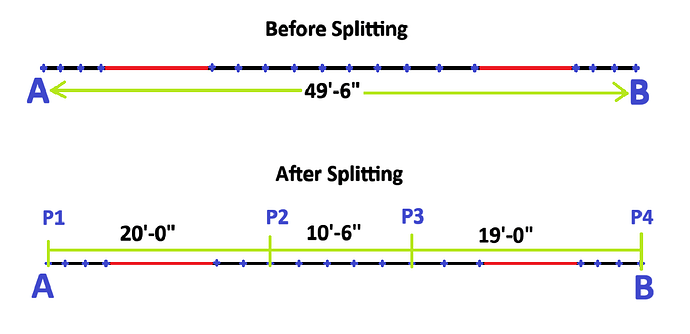
I have a long black line (Line AB), and I want to split it into parts, with each part being about 20 feet long. But I have three important rules I need to follow:
The split points must be on the either of blue points (called plus points) that are already marked along the line.
The split points must also be at least greater than or equal to 5 feet away from the red lines marked along the line.
The split line should be less than or equal to 20 feet
Where,this function should repeat till the line end point.
What I Need Help With:
I’m looking for a method or process to split the line correctly in Dynamo, considering these rules. I want to automate the process so it always follows the three conditions : splitting at the plus points and keeping at least 5 feet away from the red lines and function should repeat till the line end by maintaining the Split line length less than or equal to 20 feet.
To get the Split Line’s Start and end Points.
Any advice or Dynamo script suggestions would be greatly appreciated!
Thank you!

split
split1192×578 33.2 KB

2

Hey,

If you have a root around under Geometry > Curves > Curve, I think you’ll find lots of useful nodes.

image
image1830×1041 200 KB

You are already doing a good job of defining your rules, you just need to set them out step by step, and build up the complexity slowly.

e.g.
‘Plus Points are always 1 foot’ node: ‘Point at Segment Length’
‘There are 4 plus points before the first red line’ node: Sequence (start 0, end 4, step 1)

etc. etc.

Have a play and let us know how you get on :slight_smile:

Hope that helps,

Mark

2 Likes
3

Thanks for your reply!
The plus points on-center will vary. If we use a sequence node, it will split the line into equal parts, but the start and end points will depend on these conditions:

  • The split points must be on the blue points (called “plus points”) marked along the line.
  • The split points must be at least 5 feet away from the red lines marked along the line.
  • The split line should not be longer than 20 feet.

Here We got the first split line of the AB line using the following method:

  • We started at point A (the beginning of the AB line).
  • We added 20 feet (our preferred length) to point A, which gave us a new point.
  • We then found the nearest Plus Point (blue point) to this new point.
    • We made sure the split point was at least 5 feet away from the Red line.
      which satisfied the conditions for the first split.

Here, we are having trouble figuring out how to repeat this process until we reach the end of the AB line.
Any suggestions would be helpful!

4

Curve.ParameterAtPoint will help a lot here… assuming your blue points are pre-defined somewhere, start by removing any which are within 5 units of a red line. Then PointAtSegmentLength and MinimumItemByKey (with a distance to function) off a point at segment length should work for your first point. Then repeat the process by using a custom node, function, design script, or Python until you hit the end of your line.

1 Like
5

Hi

a first step towards a solution with Python

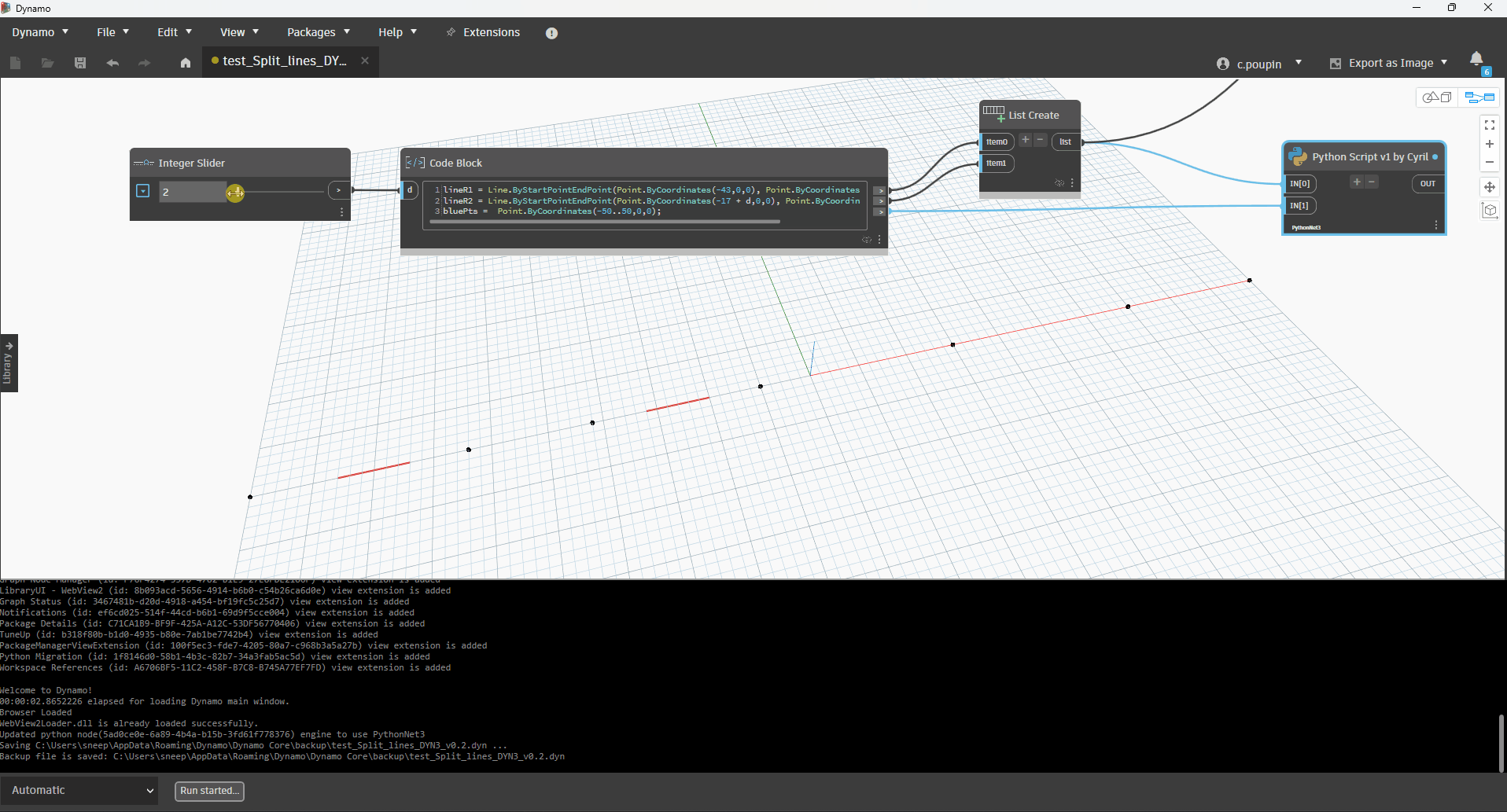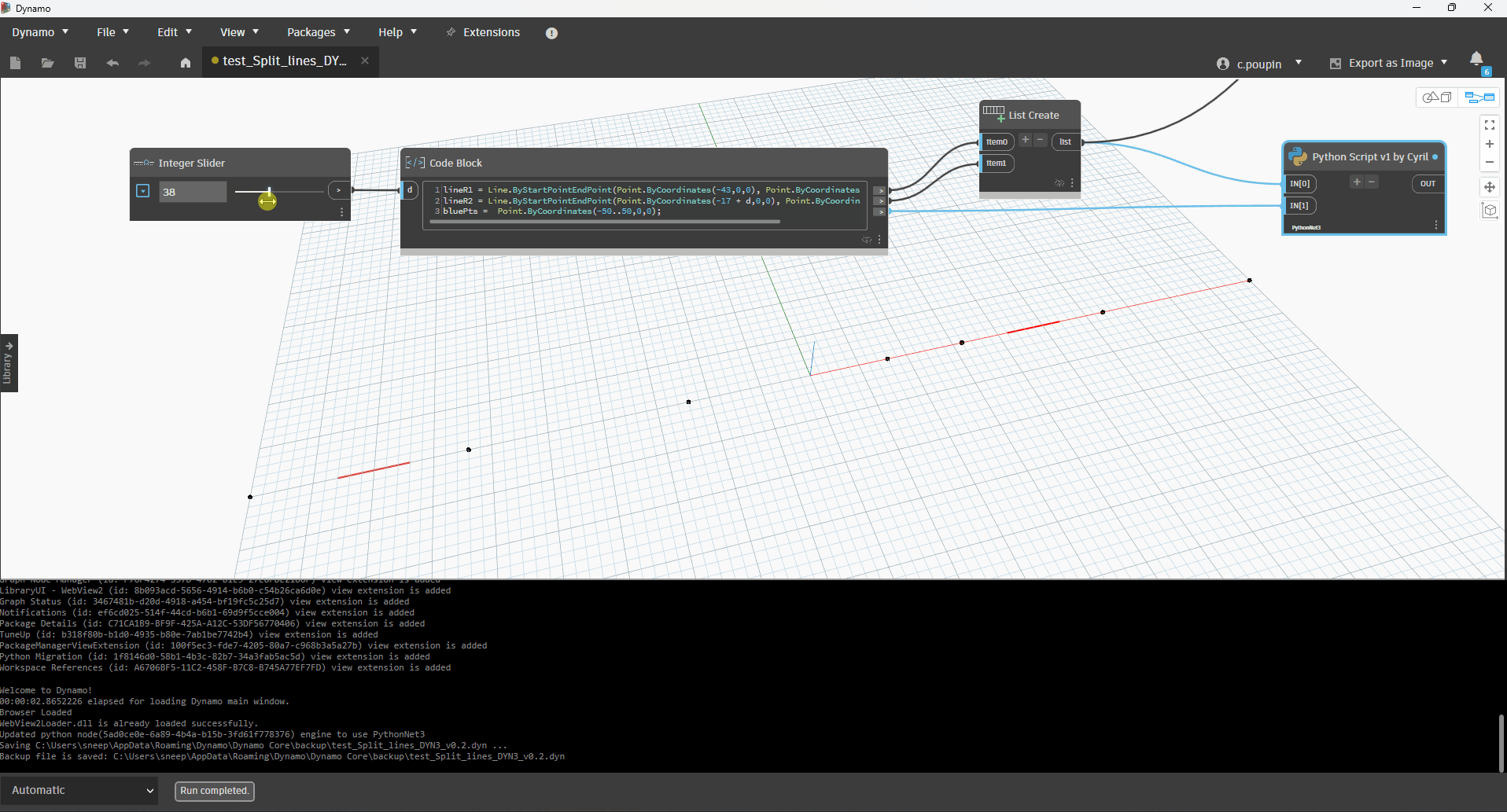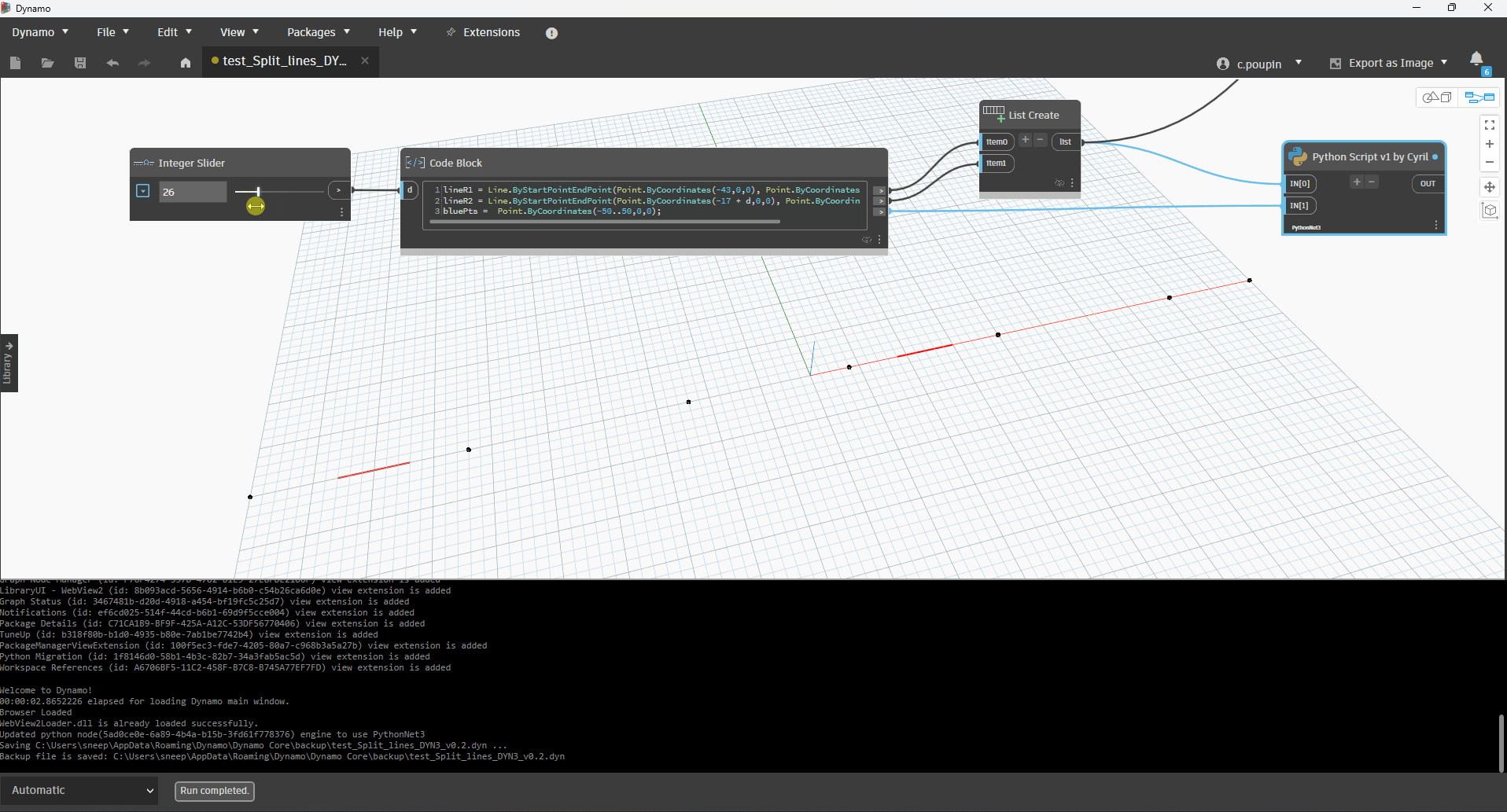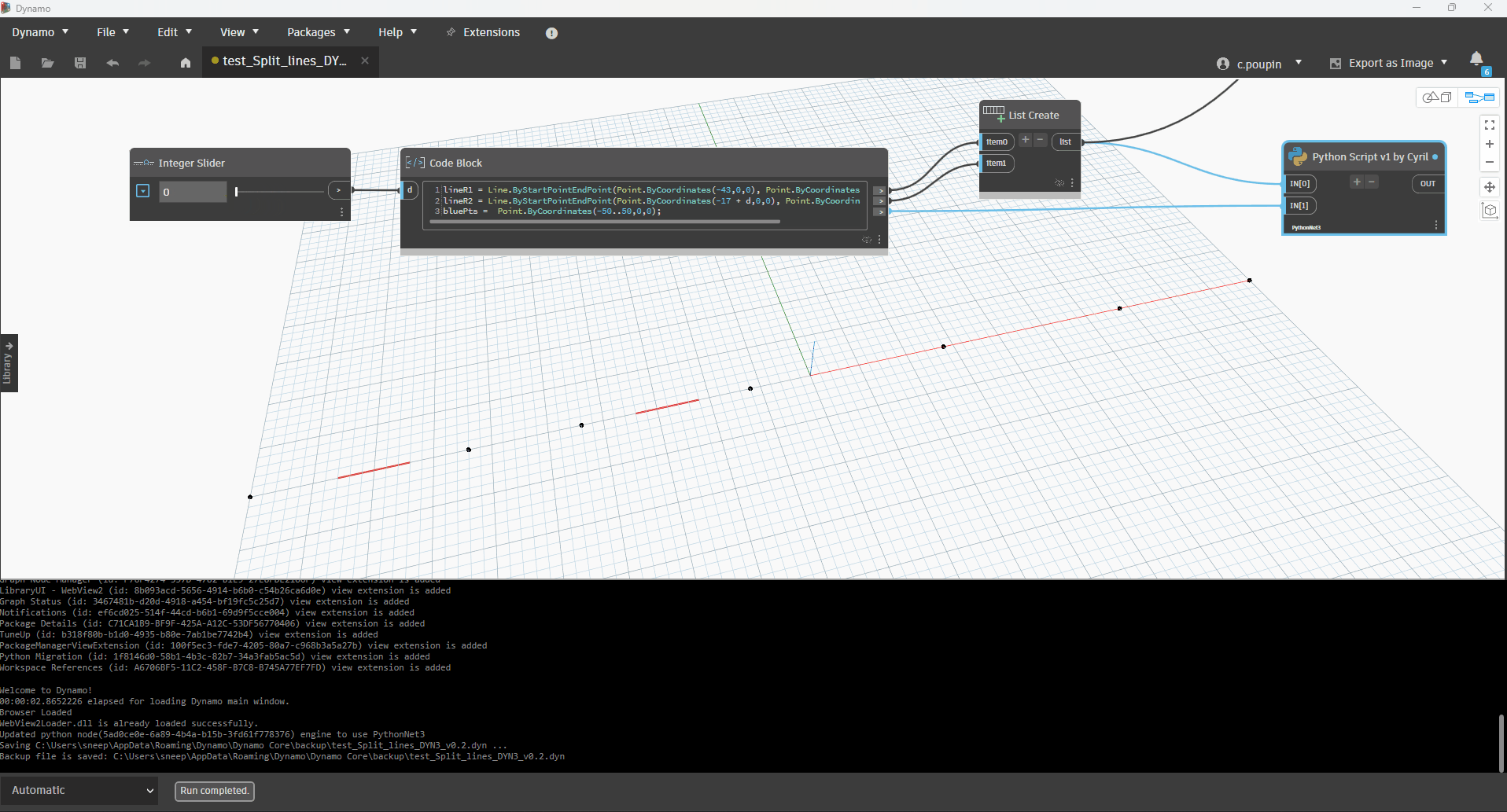
test_split_by_margin_red_line

code python

# Load the Python Standard and DesignScript Libraries
import sys
import clr
clr.AddReference('ProtoGeometry')
from Autodesk.DesignScript.Geometry import *

lst_redLines = IN[0]
lst_bluePts = IN[1]
vector_global = Vector.ByTwoPoints(lst_bluePts[0], lst_bluePts[-1]).Normalized()
margin_from_redLines = 4.5 # 5 in the forum
max_distance_between_pts = 20
pair_red_pts = []
# 1st step compute pair points for each red line
for idx, redLine in enumerate(lst_redLines):
    extendEnd = redLine.EndPoint.Add(redLine.Direction.Normalized().Scale(margin_from_redLines))
    extendStart = redLine.StartPoint.Add(redLine.Direction.Normalized().Reverse().Scale(margin_from_redLines))
    # compute a new redline with margin
    newRedLine = Line.ByStartPointEndPoint(extendStart, extendEnd)
    # remove points intersect with the newRedLine 
    copy_bluePts = [p for p in lst_bluePts if not p.DoesIntersect(newRedLine)]
    # select nearest points on each end points
    select_outStartPoint = sorted(copy_bluePts, key = lambda p : p.DistanceTo(newRedLine.StartPoint))[0]
    select_outEndPoint = sorted(copy_bluePts, key = lambda p : p.DistanceTo(newRedLine.EndPoint))[0]
    pair_red_pts.append([select_outStartPoint, select_outEndPoint])

# 2nd step compute  points between each pair points
split_points = [lst_bluePts[0]]
for idx, (start_pta, end_ptb) in enumerate(pair_red_pts):
    if split_points[-1].DistanceTo(end_ptb) <= max_distance_between_pts:
        # escape the start_pta
        split_points.append(end_ptb)
    elif split_points[-1].DistanceTo(start_pta) > max_distance_between_pts:
        nbrPts_to_add, remainder = divmod(split_points[-1].DistanceTo(start_pta), max_distance_between_pts)
        #print(f"{nbrPts_to_add=}")
        #print(f"{remainder=}")
        for _ in range(int(nbrPts_to_add)):
            newPt = split_points[-1].Add(vector_global.Scale(max_distance_between_pts))
            split_points.append(newPt)
        if split_points[-1].DistanceTo(end_ptb) <= max_distance_between_pts:
            # escape the start_pta
            split_points.append(end_ptb)
        else:
            split_points.append(start_pta)
            split_points.append(end_ptb)
        
    else:
        split_points.append(start_pta)
        split_points.append(end_ptb)
        
# final step compute the rest to the final point 
nbrPts_to_add, remainder = divmod(split_points[-1].DistanceTo(lst_bluePts[-1]), max_distance_between_pts)
for _ in range(int(nbrPts_to_add)):
    newPt = split_points[-1].Add(vector_global.Scale(max_distance_between_pts))
    split_points.append(newPt)
split_points.append(lst_bluePts[-1])

OUT = split_points